A compete pretende tornar a competição mais justa

-->

O tempo no Modo Percurso é ponderado.

O tempo de utilizadores com bikes + leves é agravado.

Utilizadores bikes + pesadas apresentam coeficientes

de agravamento + suaves.

Vê como determinamos os coficientes usando a Física.

Como é feita a conversão entre tempo real e tempo normalizado?

1 Objectivo

Encontrar a melhor forma (mais justa) de comparar os tempos dos treinos cronometrados dos vários utilizadores

Considerar como variável o peso das diversas Bicicletas. Vários estudos indicam que por cada 1 (um) kg retirado da bicicleta, o ciclista ganha 3 (três) minutos por cada km de subida.

2 Recorre-se à Ciência para ajudar a resolver este problema

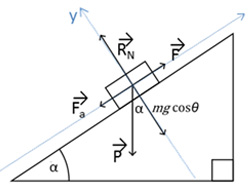
Estas são as forças envolventes: Força aplicada pelo ciclista (F), força de atrito (Fa), peso da bike sobre o solo bike (P) e reação normal da bike sobre o solo.

3 Tempo de subida e tempo de descida

Aplicando a 2ª lei do movimento de Newton: F=m*a (vectorial), é possível demonstrar que o tempo de subida e o tempo de descida são, respectivamente:

t=Δv/(F/M - g*(sin(α) + µ*cos(α))), para a subida.

t=Δv/(F/M - g*(µ*cos(α)- sin(α))), para a descida.

Δv/Δt em que Δv e Δt são a variação de velocidade e tempo. µ é o coeficiente de atrito (usa-se o dinâmico pois considera-se que o existe movimento durante a maior parte do tempo, α é o ângulo de inclinação, M é a massa da bike e g é a acelaração da gravidade.

4 Exemplo: Percurso representado em cima. 4 bikes percorrem este percurso (9, 12, 15 e 18 kg)

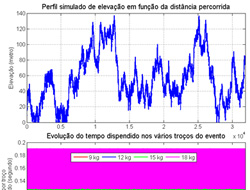
Segundo os cálculos descritos no Ponto 3, a soma dos tempos que uma bike de 9, 12, 15 e 18 kg necessitam para percorrer todo o percurso são de:

9 kg, 3132.2 segundos,

12 kg, 4247.0 segundos,

15 kg, 5406,0 segundos

18 kg, 6615.3 segundos

5 O que fazer então?

Use –se a razão entre os tempos reais do respetivo Utilizador-ciclista da bike mais pesada e o tempo real do ciclista em causa.

Como poderão dar entrada novos ciclistas ao longo de um evento (1 mês), majora-se o tempo simulado para uma bike de 22 kg. Não deverão existir muitas bikes a circular com peso (massa) superior.

6 É então ordenada a seguinte tabela:

Isto é, os tempos serão ordenados por ordem crescente dos tempos normalizados e não dos tempos reais.

A compete ajuda.

-->

Porque não haverias competir com bikes de 9 kg?

Eles passam por ti mas será que são melhores?!

E se lhes emprestares a tua bike será que fariam

melhor tempo do que tu?!

Há formas de resolver isto! A Física responde...

Actualiza o peso da tua bike no site ou app

1 Sabes como?

Acede à tua área no site da compete.

Regista-te ou entra na plataforma da compete. Os dados que necessitas são o teu Nome, username, pass para entrar na plataforma (válida para a app também), dob, e outras para facilitar o pagamento de prémios caso sejas o vencedor.

2 Acede às stores da Google/iOS para instalar a app

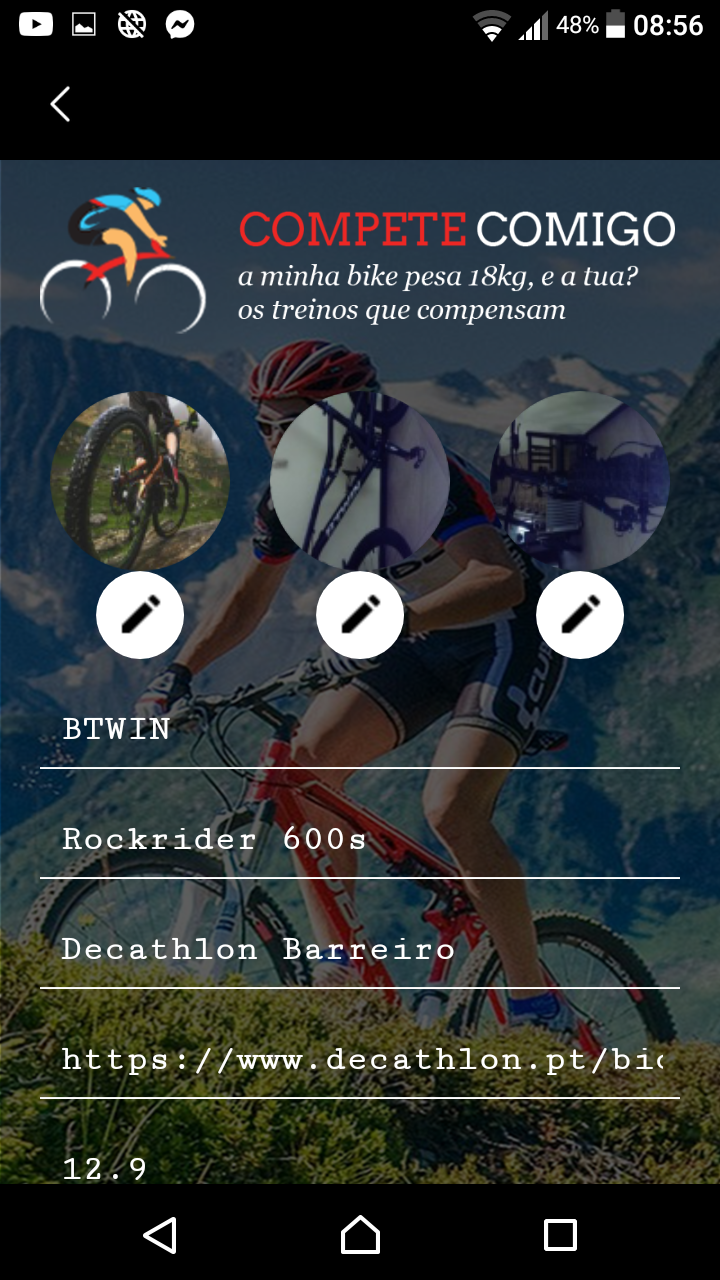
Podes registar ou entrar na tua área através do teu username e pass. A seguir, clica no ícone de menu (canto superior direito) e depois em Atualizar detalhes da bike. Deves pelo menos introduzir o peso da tua bicicleta e a comprovação de peso deverá ser efetuada através de uma fotografia ou registo oficial da marca da bike. A compete poderá a qualquer momento requerer comprovativo oficial do peso da tua bicicleta e lembra-te que deverás respeitar as regras das fotografias para que o teu percurso seja validado.

3 No site também é muito simples

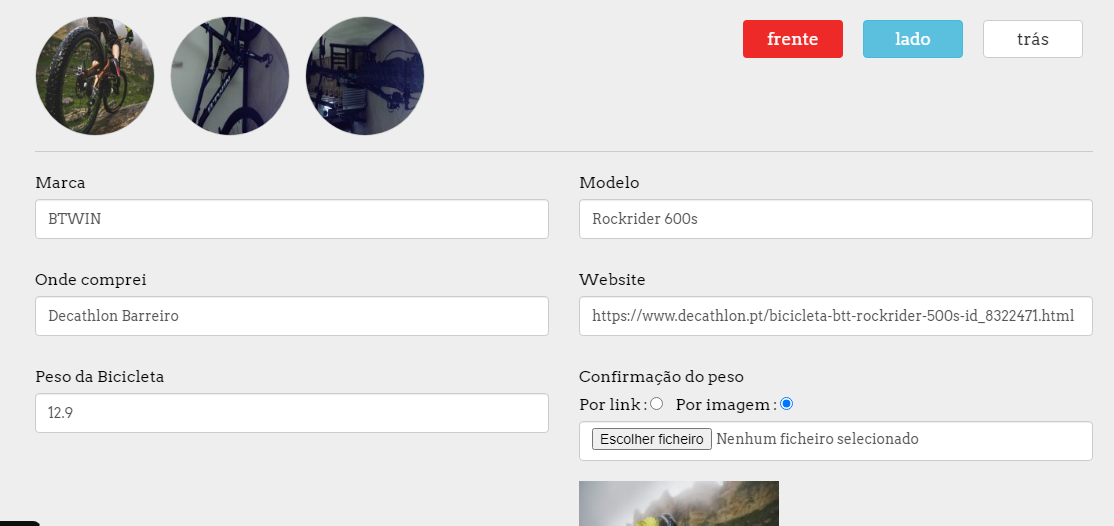
Após entrares na tua área deparas-te com o painel de controle. Acede a atualização da bike e encontras a página da figura ao lado. A compete aconselha a validares correctamente o peso da tua bicicleta pois este é um critério fundamental para o Modo de Percurso. Não tem impacto nos resultados dos Modos Livre Nacional e Internacional, porém, podes ter todo o evento pedalado (e pago!) no Modo de Percurso rejeitado por falta de validação do peso da bicicleta.

4 Alteração do peso da bicicleta após ter efetuado o percurso

A compete não aconselha a alterares o peso da tua bike após teres efetuado uma corrida do Modo de Percurso. O motivo é muito simples: ao agires dessa forma lanças desconfiança pois reparamos que só pretendeste alterar o peso da tua bicicleta com o objectivo de melhor a classificação. Pode resultar na simples eliminação dessa corrido, impedimento na participação sem reembolso no evento de Modo Percurso desse mês ou mesmo expulsão da comunidade compete. Desta forma, aconselhamos a leitura atenta dos Termos e Condições para ficares ao corrente dos teus direitos e deveres perante a comunidade de ciclistas com quem partilhas esta plataforma.

5 Boa sorte!!

Mnemónica 1: Tempo para Modo de Percurso. Vence quem fizer um pecurso pre-definido no menor tempo. Apenas conta o melhor tempo do mês relativo ao Evento.

Mnemónica 2: Distância para os Modos Livres Nacional e Internacional. Vence quem pedalar mais km acumulados durante determinado mês. Nacional: concorres contra ciclistas do teu País. Internacional: comunidade mundial da compete entra em acção e podes ganhar muito dinheiro!.

Modo Percurso disponível em:

Outros Países